Was heißt schon alt?

Chaos und Fraktale

Mitte der 80er-Jahre erreichte ein Gebiet der Mathematik die interessierte Öffentlichkeit, das bis dahin selbst vielen Mathematikern nicht vertraut war: Das Studium der Dynamischen Systeme. Eine Ursache dieser plötzlichen Popularität war das Aufkommen erschwinglicher grafikfähiger Personalcomputer, mit denen eigene Rechnerexperimente durchgeführt werden konnten. Viele Fans ließen ihre Maschinen nächtelang laufen, um am Morgen ein neues Bild zu haben, z.B. einen Ausschnitt aus dem Feigenbaumdiagramm oder einen so genannten Attraktor. Berühmt ist unter Chaos-Forschern der Lorenz-Attraktor, den der Meteorologe Edward Lorenz in den 60er-Jahren entdeckt hat. Das zwar nur scheinbar regellose aber doch schwer vorhersagbare Verhalten mancher dynamischer Systeme führte zu dem PR-trächtigen Namen Chaostheorie für dieses Gebiet. Die Verhulst-Dynamik ist ein einfaches aber aussagekräftiges Beispiel.

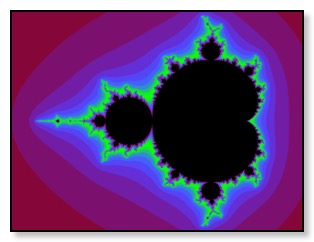
Etwa gleichzeitig entdeckte der Mathematiker Benoît Mandelbrot eine neue Form der Geometrie, die ihm besonders für die Beschreibung natürlicher Objekte geeignet schien. Er nannte sie Fraktale Geometrie und ihre Objekte Fraktale. Eine seiner bekanntesten Aussagen war: "Wolken sind keine Kugeln, Berge keine Kegel und der Blitz folgt nicht einer geraden Linie." Das berühmteste rein mathematische Fraktal war damals die hier abgebildet Mandelbrotmenge, das sog. Apfelmännchen, das bei Vergrößerung der Figur eine wesentliche Eigenschaft aller Fraktale zeigt, nämlich die Selbstähnlichkeit: Ihre Formen wiederholen sich auf allen Größenordnungen wieder und wieder, so dass jeder Teil der Figur dieselbe Komplexität wie die ganze Figur hat; ein schöner Blick in die Unendlichkeit.

Fraktale erweitern die klassische geometrische Idee der Dimension. Zu den bekannten Dimensionen eindimensional (Linie), zweidimensional (Fläche) und dreidimensional (Körper) kommen jetzt noch nicht-ganzzahlige Dimensionen (gebrochene oder eben fraktale Dimensionen), mit denen sich der Grad der Zerklüftetheit oder Rauigkeit einer Figur messen lässt. Die fraktale Dimension der britischen Küste ist z.B. anders als die der glatteren Küste von Südafrika. Beide Gebiete (Chaostheorie und Fraktale) hängen eng zusammen: Bei der graphischen Darstellung chaotischer Systeme spielen Fraktale eine wichtige Rolle. So ist die Dimension des Lorenz-Attraktors etwa 2,06. Er ist für eine ordentliche Fläche zu rauh aber ein richtiger Körper ist er auch nicht. Wir werden etwas ähnliches beim Chaos-Spiel sehen. Leider haben diese interessanten Gebiete der Mathematik und der Naturwissenschaften allgemein niemals ernsthaft den Sprung in die deutschen Lehrpläne geschafft, obwohl sich besonders die Arbeitsgruppe von Prof. Peitgen in Bremen sehr darum bemüht hat. Im Folgenden werden einige ihrer Themen exemplarisch dargestellt. Sie ermöglichen eigenes Arbeiten, Real- und Computerexperimente und sind z.T. optisch recht attraktiv.