Was heißt schon alt?

Dreieckszahlen

Figurierte Zahlen hängen - wie der Name überdeutlich sagt - mit Figuren zusammen, z.B. mit Dreiecken oder Quadraten. Sie sind nicht nur optisch ansprechend und deshalb mehr als einen Blick wert.

Dreieckszahlen und was Leibniz daraus gemacht hat

Ausgehend von einem einzelnen Punkt werden immer mehr Punkte hinzugefügt, so dass sich solche Dreiecke ergeben. Für das erste braucht man also einen einzigen Punkt, für das nächste drei, dann sechs, zehn usw. Punkte. Die Zahlen 1, 3, 6, 10, 15 usw. heißen deshalb Dreieckszahlen. Hans Magnus Enzensberger hat in seinem Zahlenteufel den Dreieckszahlen die "Fünfte Nacht" gewidmet.

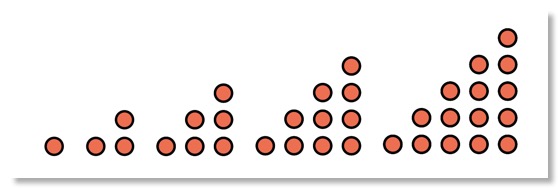
Im Sommer 2025 brachte die New York Times eine schöne kleine Reihe zu mathematischen Themen, darunter auch einen Beitrag, der mit Dreieckszahlen zusammenhängt. Genauer ging es darum, die Kehrwerte unendlich vieler Dreieckszahlen zu addieren. Zum Kontext: Eine endliche Anzahl von Summanden kann man mit dem notwendigen Aufwand immer addieren. Bei unendlich vielen Summanden ist das nicht mehr so klar. Die Summe 1 + 2 + 3 + 4 + 5 + … hat erkennbar keinen sinnvollen Wert, wenn man nicht "Unendlich" als Wert akzeptieren möchte. Was ist aber, wenn die Summanden immer kleiner werden? Ein wichtiges Beispiel ist hier die Harmonische Reihe, bei der die Kehrwerte der natürlichen Zahlen addiert werden sollen, also 1 + 1/2 + 1/3 + 1/4 + … Die werden immer kleiner. Wenn man das mit dem Taschenrechner nacharbeitet, bekommt man den Eindruck, dass sie nicht recht wachsen wollen. Vielleicht stoßen sie bei einer vernünftigen Summe an, vielleicht 3?

1 + 1/2 = 1,5000
1 + 1/2 + 1/3 = 1,8333
1 + 1/2 + 1/3 + 1/4 = 2,0833
1 + 1/2 + 1/3 + 1/4 + 1/5 = 2,2833
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 = 2,4500
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 = 2,5929
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 =2,7179
1 + 1/2 + 1/3 + 1/4 + 1/5 + 1/6 + 1/7 + 1/8 + 1/9 + 1/10 = 2,8179

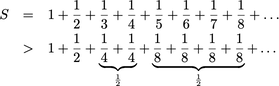
Aber der Eindruck täuscht, wie der unten dargestellte, klassischer Beweis zeigt. Ausgehend von der eigentlichen Summe werden einige Summanden verkleinert, indem der Nenner vergößert wird. Nach diesem Trick sieht man, dass sich immer wieder Summanden mit dem Wert 1/2 bilden lassen, und zwar unendlich viele davon. Das ist eine Folge der Unendlichkeit: Die Summanden gehen nicht aus. Die Summe wird also immer weiter wachen (divergieren) und keinen sinnvollen Wert annehmen. Der Trick heißt übrigens "nach unten abschätzen": Wenn schon die verkleinerte Summe immer größer wird, dann muss das auch die ursprüngliche tun.

Nun gut, vielleicht sind das doch einfach zu viele kleine Zahlen. Was geschieht, wenn man eine Auswahl trifft, z.B. als Nenner nur die Dreieckszahlen zulässt. Das sind ja immerhin viel weniger. Mit dieser Summe hat sich der bedeutende Mathematiker Gottfried Wilhelm Leibniz (1646 bis 1716) befasst. Wie üblich, ist alles ganz einfach, wenn man ein Genie ist. Leibniz ist wohl aufgefallen, dass die "löchrige" Reihe der Summanden sich regelmäßig gestalten lässt, wenn man die Brüche zerlegt. Das Resultat sieht erst einmal kompliziert aus. Hinweis: Die Brüche in den Klammern muss man gleichnamig machen, um zu erkennen, warum das Ganze funktioniert.

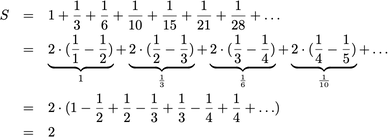
Dann kommt die Belohnung: Wenn man die 2 ausklammert, erkennt man, das von der ganzen Summe fast nichts übrig bleibt. Nur die 1 am Anfang verschwindet nicht, so dass die Summe einen ordentlichen Wert hat, nämlich 2. Diese unendliche Summe hat also einen Wert: sie konvergiert gegen den Wert 2.