Was heißt schon alt?
Broken Sticks
Mitte August 2025 berichtete Scientific American über neue Ergebnisse zum "Broken-Sticks"-Problem, von dem ich natürlich noch nie gehört hatte. Im Artikel geht es um neuere Forschungen dazu, insbesondere um einen Bezug zu den Fibonacci-Zahlen. Ich beziehe mich hier aber nur auf das ursprüngliche Problem, wie es von Martin Gardner 1956 popularisiert wurde: Ein Stab wird zufällig in drei Teile zerbrochen. Wie groß ist die Wahrscheinlichkeit dafür, dass man aus den drei Teilen ein Dreieck legen kann? Klar: Dazu muss die Summe der Längen der beiden kürzeren Teile größer sein als die Länge des längeren Teils (Dreiecksungleichung). Nun ist aber schon das mit dem "zufälligen" Zerbrechen so eine Sache und die muss zuerst geklärt werden. In der Realität wird man wohl den Stab an den Enden anfassen und er wird irgendwo in der Mitte brechen. Dann hat man die Wahl: Zerbreche ich das kürzere oder das längere Stück noch einmal? Auch das kann man dem Zufall überlassen. Wählt man aber zufällig das kürzere Teil, so gibt es sicher kein Dreieck.
Einfacher wird es so: Auf dem Stab werden zufällig und unabhängig voneinander zwei "Bruchstellen" markiert, an denen der Stab dann zerbrochen wird. Jede Kombination von Längen ist dann gleich wahrscheinlich. Dann greift eine schöne Argumentation, die sich auch im ursprünglichen Artikel von Martin Gardner findet und die auf eine Eigenart eines gleichseitigen Dreiecks (Satz von Viviani, s.u.) zurückgreift.
- (1) Zeichne ein gleichseitiges Dreieck mit Seitenlänge a und Höhe h. Sein Flächeninhalt ist A = 1/2•a•h.
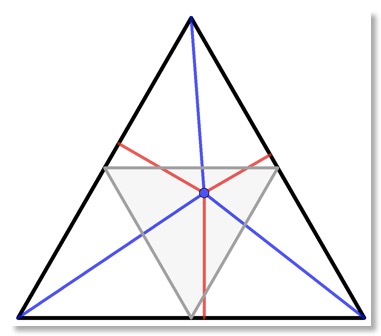
(3) Verbinde ihn mit den Ecken des Dreiecks (blaue Linien) und zeichne Lote auf die drei Seiten (rote Linien).
(4) Die blauen Linien teilen das große Dreieck in vier kleinere Dreiecke, deren Höhen (h1, h2, h3) die roten Lote sind.
(5) Für die Inhalte der vier Dreiecke gilt: A = 1/2•a•h = 1/2•a•h1 + 1/2•a•h2 + 1/2•a±h3 = 1/2•a•(h1 + h2 + h3).
(6) Daraus folgt h = h1 + h2 + h3. Die roten Strecken sind also - unabhängig von der Lage des gewählten Punktes - zusammen so lang wie die Höhe des großen Dreiecks (Satz von Viviani).
(7) Sie können deshalb für die drei Bruchstücke unseres zerbrochenen Stabes stehen.
(8) Solange der zufällig gewählte Punkt im Inneren des grauen Dreiecks (Verbindung der Seitenmitten des großen Dreiecks) liegt, ist das längste "Bruchstück" kürzer als die halbe Länge des Stabes, sodass ein Dreieck gelegt werden kann.
(9) Der Inhalt des grauen Dreiecks ist ein Viertel des Inhalts des großen Rechtecks. Die gesuchte Wahrscheinlichkeit ist also 1/4.
Anmerkung 1: Auf den Satz von Viviani hat mich ChatGPT gebracht (Ende 2025). Ich kannte den nicht. Überhaupt finde ich ChatGPT bei konkreten Fragen als Ansatzpunkt sehr hilfreich.
Anmerkung 2: Für das realitätsnähere Zerbrechen habe ich mit meinem PicoCalc ein BASIC-Programm geschrieben. Eine Beschreibung folgt - vielleicht.