Was heißt schon alt?

Vom Dreieck zum Quadrat - und zurück

Am 27. März 2025 berichtete Scientific American über die Lösung eines 122 Jahre alten Rätsels, dass auf eine Idee des Rätselkönigs Henry Dudeney zurückgeht. Ein gleichseitiges Dreieck soll durch möglichst wenige geradlinige Schnitte so zerlegt werden, dass es zu einem Quadrat zusammengesetzt werden kann. Das funktioniert mit vier Teilen z.B. so:

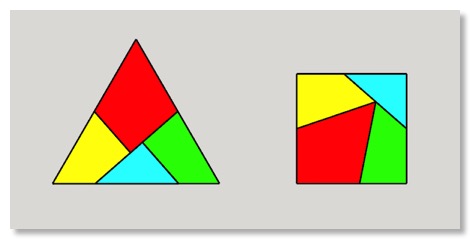
Die Meldung am 27. März bezog sich darauf, dass der japanische Mathematiker Tonan Kamata zusammen mit zwei anderen Mathematikern bewiesen hat, dass es keine Teilung mit weniger als vier Teilen gibt. Eine weitere Besonderheit dieser Teilung ist, dass man die vier Teile so mit Gelenken verbinden kann, dass Dreieck und Quadrat ineinander verwandelt werden können. Im SciAm-Artikel gibt es eine schöne Animation dazu. Ich wollte das Ganze natürlich verstehen, nacharbeiten und schließlich als 3D-gedrucktes Objekt in der Hand halten. Hier die Schritte:

1 Konstruktion eines flächengleichen Quadrates zu einem gleichseitigen Dreieck

Das ist Schulmathematik! Nach dem Höhensatz im rechtwinkligen Dreieck, ist das Quadrat über der Höhe flächengleich mit dem Rechteck, das aus den beiden Hypotenusenabschnitten gebildet werden kann: "h Quadrat gleich p mal q". Die Höhe des Dreiecks ist ein Hypotenusenabschnitt, die halbe Grundseite der zweite,. Über beiden zusammen wird mit dem Thaleskreis ein rechtwinkliges Dreieck konstruiert. Seine Höhe ist dann die Seitenlänge des gesuchten Quadrates.

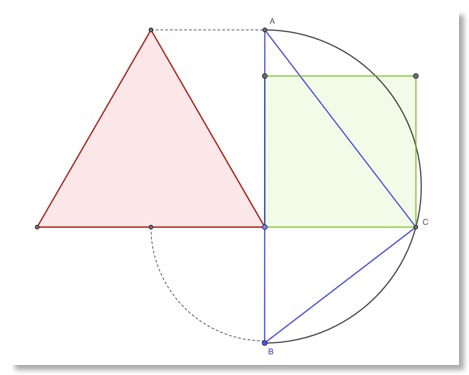
2 Zerlegung des Dreiecks oder des Quadrates

Das ist keine Schulmathematik und ich musste etwas suchen. Dann war ich überrascht, wieviel Literatur es zu geometrischen Zerlegungen gibt. Es scheint ein Tummelplatz von Hobbyisten (gewesen) zu sein. Ich habe das Buch "Recreational Problems in Geometric Dissections & How To Solve Them" von Harry Lindgren (gibt's im Netz) verwendet. Die Zeichnung illustriert die Idee.

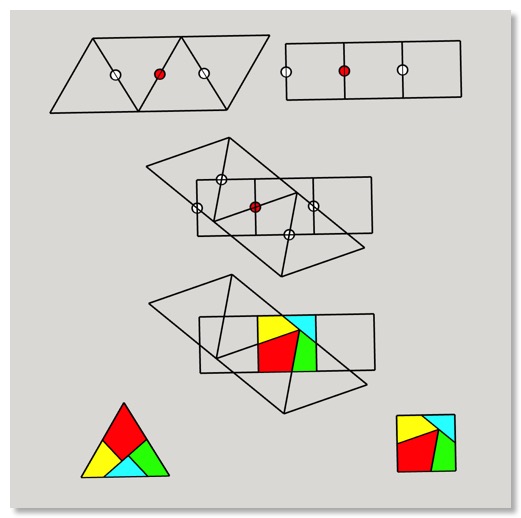
Aus den beiden Figuren wird je ein Streifen gebildet. Die markierten Punkte sind jeweils Symmetriepunkte (Punktsymmetrie) aufeinanderfolgender Figuren. Zwei davon (rot markiert) werden übereinander gelegt. Dann wird einer der Streifen (hier der Dreiecksstreifen) so gedreht, dass Symmetriepunkte und Kanten der beiden Streifen zusammentreffen. Das mittlere Quadrat ist jetzt wie gewünscht zerlegt.

3 Konstruktion und Druck

Ich zeichne mit Sketchup, weil ich das Programm jetzt schon lange kenne. Auch die Zeichnung in Punkt 2 ist in Sketchup entstanden, so dass ich einfach mit den gefärbten Teilen weiterarbeiten konnte. Wie oben erwähnt, kann man die vier Teile mit Gelenken verbinden. Zunächst hatte ich an eine "Schraubversion" gedacht. Das war mir zu wackelig - also Presspassung. Nachteil: Funktioniert bei meinem Drucker (Flashforge Adventurer 4 Pro) vielleicht aber nicht bei anderen. Ich habe sowohl die Sketchup-Datei als auch die stl-Dateien in den Download-Bereich gestellt.

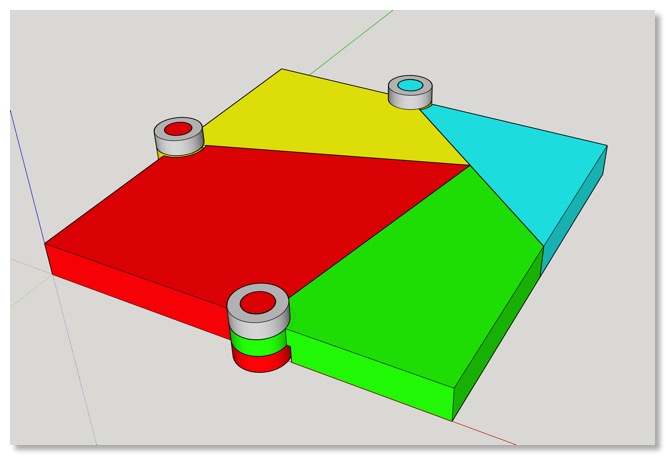
4 Die Realität

Das Quadrat hat eine Kantenlänge von etwa 11cm und bisher funktioniert die Mechanik ohne Wackeln gut.